Nancy Hingston Celebration

30-31 October 2025

url

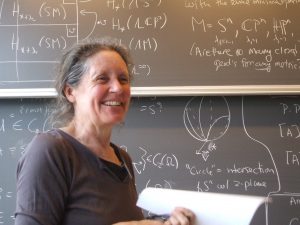This is a conference to celebrate the work and influence of Nancy Hingston in geometry and topology. 

 

 

Kai Cieliebak

Tobias Colding (tbc)

Basak Gurel

Dusa McDuff

Florian Naef

Hans-Bert Rademacher

Manuel Rivera

Maximilian Stegemeyer

 

 

 

 

 

 

 

Thursday Friday
9:00 Registration
10:00 Talk Talk
10:45 Coffee Coffee
11:15 Talk Talk
12:00 Lunch Lunch
14:00 Talk

Talk
14:45 Coffee Coffee and cake
15:15 Talk Talk
16:00

Cake
16:30

Gong show
18:30

Dinner

 

 

 

 

 

 

 

 

 

Venue in central Copenhagen TBA. 

 

 

 

 

 

 

We kindly ask the participants to arrange their own accommodation.

We recommend Hotel 9 Små Hjem, which is pleasant and inexpensive and offers rooms with a kitchen. Other inexpensive alternatives are Steel House Copenhagen (close to city centre), and CabInn, which has several locations in Copenhagen: the Hotel City (close to Tivoli), Hotel Scandinavia (Frederiksberg, close to the lakes), and Hotel Express (Frederiksberg) are the most convenient locations; the latter two are 2.5-3 km from the math department. Somewhat more expensive – and still recommended – options are Hotel Nora and  Ibsen's Hotel.

An additional option is to combine a stay at the CabInn Metro Hotel with a pass for Copenhagen public transportation (efficient and reliable). See information about tickets & prices.

 

 

 

 

 

 

 

 

 

 

 

 

Please fill in the registration form. 
Deadline for registration is September 29th 2025.

 

 

 

 

 

 

 

 

 

 

Organisers: Alexandru Oancea and Nathalie Wahl