Harald Bohr Lecture by Sir Andrew Wiles
The Department of Mathematical Sciences is immensely proud to announce Sir Andrew Wiles, the Royal Society Research Professor at the University of Oxford, as the next distinguished Harald Bohr lecturer. His lecture, titled "Rational points on elliptic curves", takes place on Wednesday, March 14 at 15:15 in Auditorium 1.
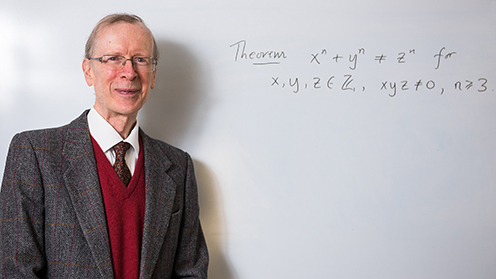
Sir Andrew Wiles. Photo: www.johncairns.co.uk
Sir Andrew Wiles presents his lecture as "a survey of the progress on finding and describing the rational points on elliptic curves". This special event also marks the revival of the Abel Prize Lecture Series, hosted together with the Danish Mathematical Society.
The Norwegian Academy of Science and Letters awarded the Abel Prize for 2016 to Sir Andrew Wiles for "his stunning proof of Fermat’s Last Theorem by way of the modularity conjecture for semistable elliptic curves, opening a new era in number theory".
Andrew Wiles first became aware of Fermat's Last Theorem as a young boy: "I grew up in Cambridge, and my love of mathematics dates from those early childhood days. I loved doing problems in school. I'd take them home and make up new ones of my own. But the best problem I ever found, I found in my local public library. I was just browsing through the section of math books and I found this one book, which was all about one particular problem - Fermat's Last Theorem. This problem had been unsolved by mathematicians for 300 years. It looked so simple, and yet all the great mathematicians in history couldn't solve it. Here was a problem, that I, a 10-year-old, could understand, and I knew from that moment that I would never let it go. I had to solve it."
"There is no other problem that will mean the same to me. This was my childhood passion. There’s nothing to replace that. I had this very rare privilege of being able to pursue in my adult life what had been my childhood dream. I know it’s a rare privilege, but if you can tackle something in adult life that means that much to you, then it’s more rewarding than anything imaginable."
"Fermat’s Last Theorem, first formulated by Pierre de Fermat in the 17th century, is the assertion that the equation x^n + y^n = z^n has no solutions in positive integers for n>2. Fermat proved his claim for n=4, Leonhard Euler found a proof for n=3, and Sophie Germain proved the first general result that applies to infinitely many prime exponents. Ernst Kummer’s study of the problem unveiled several basic notions in algebraic number theory, such as ideal numbers and the subtleties of unique factorization. The complete proof found by Andrew Wiles relies on three further concepts in number theory, namely elliptic curves, modular forms, and Galois representations." (Excerpts from the citation by the Abel Committee).
Andrew Wiles studied mathematics in Oxford, obtaining a Bachelor's degree in 1974 from Merton College. A year later, he entered Clare College in Cambridge to study for his doctorate under the supervision of John Coates, who was working on the Iwasawa theory of elliptic curves. Between 1977 and 1980, Wiles was a Junior Research Fellow at Clare College, Cambridge and also a Benjamin Pierce Assistant Professor at Harvard University. He obtained his PhD in 1980: his doctoral thesis concerned another famous problem, the conjecture of Birch and Swinnerton-Dyer. He became a professor at Princeton University in 1982, where he remained for almost 30 years, being appointed as the Eugene Higgins Professor of Mathematics in 1994. The following year, his paper which proves Fermat's Last Theorem, titled "Modular elliptic curves and Fermat's Last Theorem", appeared in the Annals of Mathematics. In 2011, he moved to Oxford as a Royal Society Research Professor.

Andrew Wiles outside the Mathematical Institute at Oxford University, the building is named in his honor. Photo: www.johncairns.co.uk
For his outstanding work, considered to be "one of the greatest triumphs of contemporary mathematics" and "a monument to individual perseverance", Andrew Wiles received numerous awards, including the Fermat Prize (1995), the Ostrowski Prize (1995), the Cole Prize (1996), the Wolf Prize (1995/96), the Royal Medal of the Royal Society (1996), the Wolfskehl Prize (1997). In 1989 he became a Fellow of the Royal Society and in 1996, a foreign member of the National Academy of Sciences of the United States. In 1998, not being eligible for the award of a Fields medal on the grounds that he was over forty years of age, the International Mathematical Union presented him with a silver plaque at the International Congress of Mathematicians, Berlin. In 1999 he received the Clay Research Award "for his role in the development of number theory". In 2000 he received a knighthood from the Queen of England. Sir Wiles also received the Shaw Prize (2005), and the Copley Medal 2017 of the Royal Society, in addition to the Abel Prize (2016).
"I want people to think of mathematics as this beautiful edifice which is immutable, the most permanent thing there is, besides it being tremendously useful since it is the language of science and it underlines everything." (Oxford Mathematics London Public Lecture - Andrew Wiles in conversation with Hannah Fry, December 2017).
Magdalena Musat
More on Sir Andrew Wiles:
- Ad Honorem: Sir Andrew J. Wiles , Notices of the American Mathematical Society, March 2017, Vol 64, Issue 03
- See photos from the lecture
Harald Bohr Lectures

The Harald Bohr Lectures are named after the distinguished Danish mathematician Harald Bohr (1887-1951), to honor his legacy as an eminent and passionate communicator of mathematics. The Harald Bohr lecturers are outstanding mathematicians from both pure and applied mathematics.
The lectures are held 1-3 times per year. The Harald Bohr lecture series is organized by Magdalena Musat.

